2次不等式がある区間で常に成り立つ条件の問題を解けるようになろう!!
おはようございます!
godfaです!
今回は「数ⅠAの復習」
ということで
「2次不等式の問題」
について紹介します!!
今回は特に
「2次不等式が
ある区間で
常に成り立つ条件」
についての問題を
紹介します!
2次不等式に関する問題が
なんでそうなるのか
分からない
と感じるそこのあなた!

この記事を読んで、
解き方を理解しましょう!
この記事を読めば、
2次不等式に関する問題が
分かるようになり
応用問題への理解にも繋がります!
しかし、
この記事を読まないと
2次不等式に関する問題の
応用問題が難しいままかも
それでは紹介していきます!
この解き方を実践すれば
どんな2次不等式に
関する問題でも
しっかり対応することが出来ます!

この方法は
青チャートにも
記載されている方法です!!!
最も大切なこととして
グラフを書いて
可視化する!!
ということです!
今回の
「ある区間で常に成り立つ」
問題は場合分けすることが
ほとんどです!
なので
その全ての
グラフをかけると
解法が見え
正確な回答を
書くことが出来ます!
わからなく
解くのが難しいと
感じたら
まず、
グラフを書いてみましょう!

頭の中でイメージする
だけでなく、
しっかりグラフを書き
目でも理解することが
大切です!
どんな問題でも
大切なのは
グラフを書き、
可視化することです!!
例を見て見ましょう!
「0<=x<=8のすべてのxに対して、不等式x^2-2mx+m+6>0が成り立つような定数mの値の範囲を求めよ。」
という問題です!
まずは、
ヒントが少ないので
二次関数y=x^2-2mx+m+6
とおいて
基本形に直してみましょう!
すると
このようになります!

上に凸で
頂点が変化するグラフ
ということが分かります!
では
0<=x<=8の範囲で
グラフは
どんなパターンがあるのか
考えていきます
すると
この3パターンが
思いつくと思います!
①範囲がグラフの
左側にあるパターン
②範囲がグラフの
真ん中にあるパターン
③範囲がグラフの
右側にあるパターン
それぞれグラフを
書いてみるとこんな感じ!

この3つの
グラフを見ると
この3パターンについて
記述出来れば
正確な解答ができるな
とイメージすることが出来ます!
あとは
それぞれについて
記述していくだけです!
最後に
しっかり
解答を書けば完成です!!

これであなたも
2次不等式の問題ついて
しっかり
理解出来ましたね!
今からでも
できることとして
イメージを
グラフにしてみる!
ことを心がけましょう!!
これは
二次関数の問題の
多くで使える方法です!
イメージを
可視化することが出来れば
問題もしっかり
理解できます!
解法の手助けにも
繋がります!!
頑張っていきましょー!!
2次不等式解法のコツを学び、解けるようになろう!!
おはようございます!
godfaです!
今回は「数ⅠAの復習」
ということで
「2次不等式の問題」
について紹介します!!
2次不等式に関する問題
なんでそうなるのか
分からない
と感じるそこのあなた!

この記事を読んで、
解き方を理解しましょう!
この記事を読めば、
2次不等式に関する問題が
分かるようになり
応用問題への理解にも繋がります!
しかし、この記事を読まないと
2次不等式関する問題の
応用問題が難しいままかも
それでは紹介していきます!
この解き方を実践すれば
どんな2次不等式に
関する問題でも
しっかり対応することが出来ます!

この方法は
青チャートにも
記載されている方法です!!!
まず大切な知識として
2次不等式の解について

これは
しっかり覚えましょう!!
プラスで!
最も大切なこととして
グラフを書いて
可視化する!!
ということです!
頭の中でイメージする
だけでなく、
しっかりグラフを書き
目でも理解することが
大切です!!
簡単な例です!
「次の2次不等式を解け。
x(x-3)<0」
これはこんな感じ!!

どんな問題でも
大切なのは
グラフを書き、
可視化することです!!
例を見て見ましょう!
「次の事柄が成り立つように、
定数a,bの値を定めよ。
2次不等式
ax^2+bx+3>0の解が
-1<x<3である。」
という問題です!
まずは、
ヒントが少ないので
二次関数y=ax^2+bx+3と考えて
グラフに書いてイメージしてみましょう!

するとこの2つがかけると思います!
今回は解が-1<x<3なので
グラフを見比べて
解を満たす
上に凸の放物線を
選びます!
あとは
条件を見つけて
解いていくだけ!
今回は上に凸のグラフ
なので a<0 です!
また
グラフより(-1,0)と(3,0)を
通るので
二次関数y=ax^2+bx+3に
代入して
最後にこれを解けばOK!!

最後に
しっかり
解答を書けば完成です!!

これであなたも
2次不等式の問題ついて
しっかり
理解出来ましたね!
今からでも
できることとして
イメージを
グラフにしてみる!
ことを心がけましょう!!
イメージを
可視化することが出来れば
問題もしっかり
理解できます!
解法の手助けにも繋がります!!
頑張っていきましょー!!
放物線とx軸の共有点の個数の解法をしっかり理解しよう!!
おはようございます!
godfaです!
今回は「数ⅠAの復習」
ということで
「放物線とX軸の共有点の個数問題」
について紹介します!!
放物線とX軸の共有点の
個数に関する問題
なんでそうなるのか
分からない
と感じるそこのあなた!

この記事を読んで、
解法の流れと意味を理解しましょう!
この記事を読めば、
放物線とX軸の共有点の
個数に関する問題が
分かるようになり
応用問題への理解にも繋がります!
しかし、この記事を読まないと
放物線とX軸の共有点の
個数に関する問題の
応用問題が難しいままかも
それでは紹介していきます!
この解き方を理解すれば
どんな放物線とX軸の共有点の
個数に関する問題でも
しっかり対応することが出来ます!

この方法は
青チャートにも
記載されている方法です!!!
まず1番大切な知識として
二次関数のグラフと
X軸の位置関係の性質です!
これはしっかり覚えましょう!!

あとは
二次関数y=ax^2+bx+cを
二次方程式ax^2+bx+c=0として
判別式Dと0の
大小関係を見ればOK!!
解き方はたったこれだけです!!
ここで、この性質を
しっかり理解しましょう!
この性質は
すばり
頂点がどこにあるか!です!
例えば
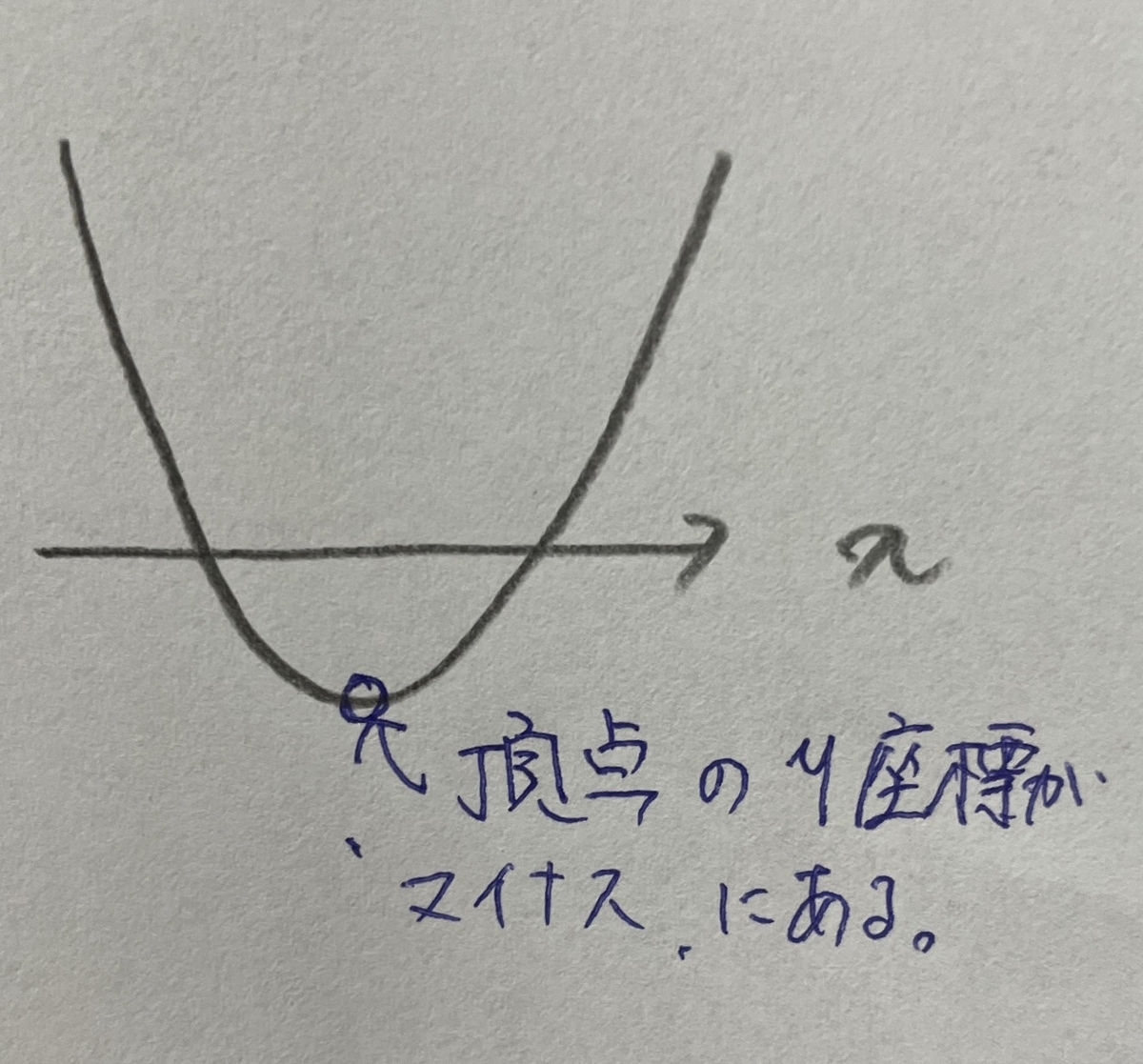
下に凸のグラフで
頂点のy座標が
マイナスにあれば
X軸との交点は2つ出来ます。
また、
下に凸のグラフで
頂点のy座標が
0なら
X軸とは接しますよね!

最後に
下に凸のグラフで
頂点の座標が
プラスにあれば
X軸との交点は無くなります!

二次関数のグラフと
X軸の位置関係は
この頂点の
位置を使った性質なんです!
ここで、なんで判別式を
使うのか言うと
一般形を基本形に直した時

こんな形になります!
お気づきの通り
判別式Dの部分が
出てきますよね!
ここで頂点の座標は

のようになります!
あとはDが0より
大きいか等しいか小さいかを
見比べれば
位置関係がわかります!!
位置関係が分かれば
X軸との共有点の
個数も見えてきますね!
時間に余裕があれば
グラフを書くと
確認できるのでなおよし!!です!!
あとは、解答を作るだけ!!
例を見て見ましょう!
「放物線y=x^2-4x+kと
X軸の共有点の個数は、
定数のkの値によって
どのように変わるのか。」
という問題です!
まず、
放物線y=x^2-4x+kを
x^2-4x+k=0として
判別式をDとします!
今回はxの係数が
2の倍数なので
D/4を使い計算を
楽にしましょう!

あとは
D/4と0の関係を
見るだけ!!
見てみるとこんな感じ!

最後に
しっかり
解答を書けばOK!!

ちなみに
グラフはこんな感じ!

kの値で頂点の位置が
変わっていることが
分かります!!
これであなたも
放物線と
X軸の共有点の個数の
解法について
しっかり理解出来ましたね!
今からでもできることとして!!
二次関数のグラフと
X軸の位置関係の性質を
しっかり覚えましょう!!!
覚えている+理解している
があれば、
応用問題も怖くありません!!
これからもしっかり
頑張っていきましょうー!!
二次関数決定③ 正しい解法でスラスラ解けるようになろう!
おはようございます!
godfaです!
今回は「数ⅠAの復習」
ということで
「二次関数の決定問題」
について紹介します!!
二次関数の決定する問題
どうやって解けばいいのか
わからないと
感じるそこのあなた!

この記事を読んで、
解き方を身につけましょう!!
この記事を読めば、
二次関数の決定する問題が
すぐ解けるようになります!!
しかし
この記事を読まないと
二次関数の決定する問題に
時間を費やしてしまうかも、、、
二次関数の決定する問題には
主に3種類あります!
①頂点や軸に関する条件が
与えられる
②最大値や最小値が
与えられる
③グラフが通る3点が
与えられる
今回は③を紹介します!!!

この解き方を身につければ
どんな二次関数の決定する問題でも
しっかり対応することが出来ます!
この方法は
青チャートにも
記載されている方法です!!!
③グラフが通る3点が与えられる場合
すばり!!
一般形!
y=ax^2+bx+c を使おう!!!
グラフを
通る3点の条件から
3つの文字式を作ろう!!
あとは
この3つの文字式を使って
連立方程式を解くだけ!!

3つの文字がある時は
その3つの文字を含む式が
3つあれば解くことができます!
また
「通る」と
問題文に書いてあれば
「代入する!」と
解釈しよう!
時間に余裕があれば
グラフを書くと
確認できるので
なおよし!!です!!
あとは、解答を作るだけ!!
例を見て見ましょう!
「二次関数のグラフが
次の条件を満たすとき、
その二次関数を求めよ。
3点(-1,16),(4,-14),(5,-8)を通る。」
という問題です!
まず初めに
グラフが通る3点が
与えられる場合は
一般形 y=ax^2+bx+c
次に3点を「通る」ので
3点を一般形に代入して
3つの文字式を作ろう!

あとは連立方程式を解くだけ!!

最後に
しっかり
解答を書けばOK!!

この流れを覚えれば
誰でもスラスラ
解けるようになります!!
これであなたも
二次関数の決定する問題が
3つ解けるようになりました!!
今からでもできることとして!
3点が与えられたら
一般形 y=ax^2+bx+cを
しっかり覚えましょう!!
その後この方法を使えば
二次関数の決定する問題も
スラスラ解けるようになります!!
二次関数決定② 正しい解放でスラスラ解けるようになろう!!
おはようございます!
godfaです!
今回は「数ⅠAの復習」
ということで
「二次関数の決定問題」
について紹介します!!
二次関数の決定する問題
どうやって書けばいいのか
わからないな
と感じるそこのあなた!

この記事を読んで、
書き方を
身につけましょう!!
この記事を読めば、
二次関数の決定する問題が
すぐ解けるようになります!!

しかし、この記事を読まないと
二次関数の決定する問題に
時間を費やしてしまうかも、、、
二次関数を
決定する問題には
主に3種類あります!
①頂点や軸に関する条件が
与えられる
②最大値や最小値が
与えられる
③グラフが通る3点が
与えられる
今回は②を紹介します!!!
この解き方を身につければ
どんな二次関数を
決定する問題でも
しっかり
対応することが出来ます!
この方法は
青チャートにも
記載されている方法です!!!
②最大値や最小値が
与えられる場合
すばり!!
基本形
y=a(x-p)^2+q を使おう!!!
最大値や最小値の条件から
グラフの概形を読み取ろう!!
主に
上に凸か下に凸かを
判断しよう!
簡単にグラフの概形を
書くと
より分かりやすくなります!!

概形が読み取れたら
最大値や最小値のヒントから
頂点を見つけよう!!!
あとは
他に与えられた条件を使い
解いてくだけ!!!
また
「通る」と問題文に
書いてあれば
「代入する!」と解釈しよう!
時間に余裕があれば
グラフを書くと
確認できるので
なおよし!!です!!
あとは、解答を作るだけ!!
例を見て見ましょう!
「1<=x<=5の範囲で、
x=2のとき最大値2をとり、
最小値が-1である
二次関数を求めよ。」
という問題です!
まず初めに
最大値や最小値に関する条件が
与えられたら
基本形 y=a(x-p)^2+q
次に概形を判断しよう!!
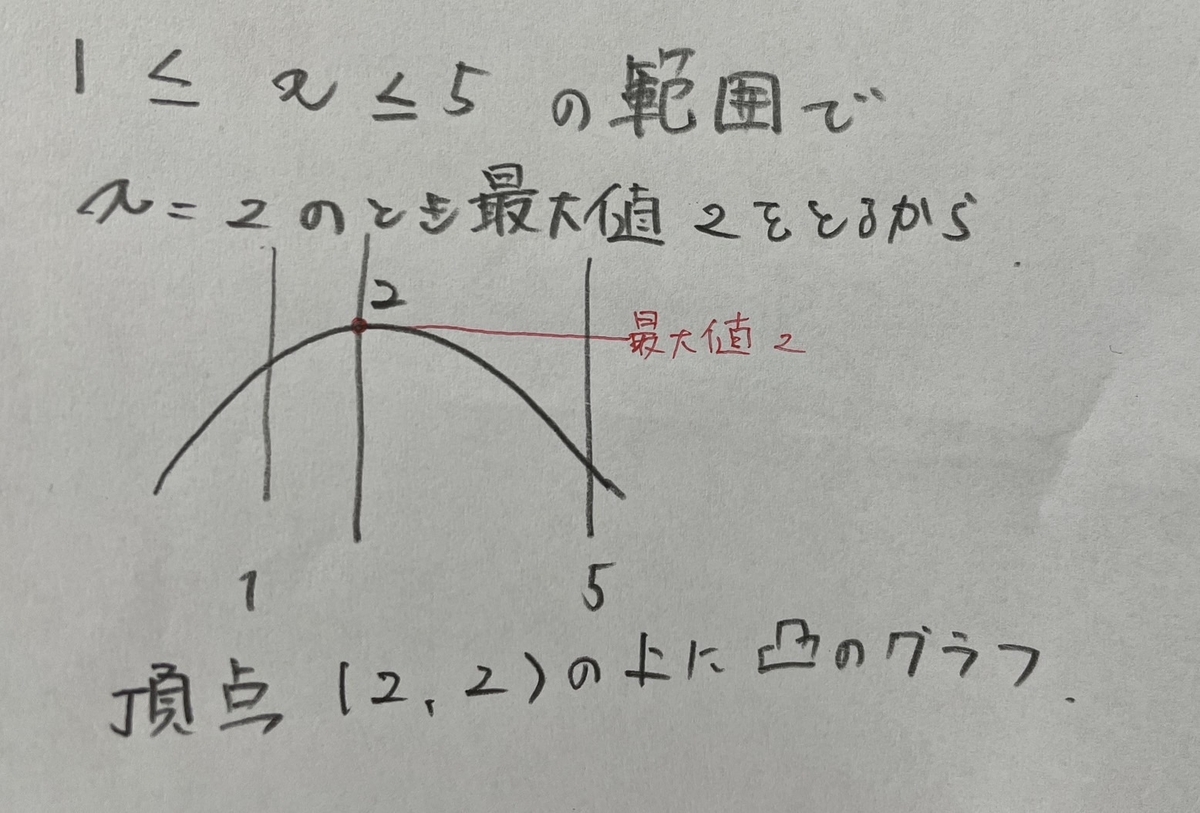
今回上に凸!!
そこから、
頂点を読み取って
文字式を作ります!!

次に
最小値が-1という
条件をつかい
文字式を解きます!!

最後に
しっかり
解答を書けばOK!!

この流れを覚えれば
誰でもスラスラ
解けるようになります!!
これであなたも
二次関数を
決定する問題が
2つ解けるようになりました!!
今からでも
できることとして!!
最大値や最小値の
条件と来たら
基本形y=a(x-p)^2+qを
しっかり覚えましょう!!!
その後この方法を使えば
二次関数の決定する問題も
スラスラ
解けるようになります!!
二次関数決定① 正しい解放ですらすら解けるようになろう!!
おはようございます!
godfaです!
今回は「数ⅠAの復習」
ということで
「二次関数の決定問題」
について紹介します!!
二次関数の決定する問題
どうやって書けばいいのか
わからないな
と感じるそこのあなた!

この記事を読んで、
書き方を
身につけましょう!!
この記事を読めば、
二次関数の決定する問題が
すぐ解けるようになります!!
しかし
この記事を読まないと
二次関数の決定する問題に
時間を費やしてしまうかも、、、
二次関数を
決定する問題には
主に3種類あります!
①頂点や軸に関する条件が
与えられる
②最大値や最小値が
与えられる
③グラフが通る3点が
与えられる
今回は①を紹介します!!!

この解き方を身につければ
どんな二次関数を
決定する問題でも
しっかり
対応することが出来ます!
この方法は
青チャートにも
記載されている方法です!!!
①頂点や軸に関する条件が
与えられた場合
すばり!!
基本形
y=a(x-p)^2+q を使おう!!!
基本形に
頂点や軸に関する
条件を代入して
文字式を作る!!
あとは
他に与えられた条件を使い
解いてくだけ!!!

また
「通る」と問題文に
書いてあれば
「代入する」と
解釈しよう!!
時間に余裕があれば
グラフを書くと
確認できるので
なおよし!!です!!
あとは、解答を作るだけ!!
例を見て見ましょう!
「二次関数のグラフが
次の条件を満たすとき、
その二次関数を求めよ。
頂点が点(-2,1)で、
点(-1,4)を通る。」
という問題です!
まず初めに
頂点、軸に関する条件が
与えられたら
基本形 y=a(x-p)^2+q
基本形に
頂点、軸に関する条件を
代入して
文字式を作ろう!!

次に
「通る」ときたら
代入しよう!!!

最後に
しっかり
解答を書けばOK!!

この流れを覚えれば
誰でもスラスラ
解けるようになります!!
これであなたも
二次関数を
決定する問題が
1つ解けるようになりました!!
今からでも
できることとして!!
頂点、軸に関する
条件と来たら
基本形y=a(x-p)^2+qを
しっかり覚えましょう!!!
その後この方法を使えば
二次関数の決定する問題も
スラスラ
解けるようになります!!
二次関数の最大値問題(範囲を動かすパターン)の書き方を学び、得点源にしよう!!
おはようございます!godfaです!
今回は「数ⅠAの復習」ということで
「二次関数の最大値問題の
範囲が動くパターン」
について紹介します!!
二次関数の最大値を求める問題
どうやって書けばいいのかわからないな
と感じるそこのあなた!

この記事を読んで、
書き方を身につけましょう!!
この記事を読めば、
二次関数の最大値問題が
得点源になります!!
しかし、この記事を読まないと
二次関数の最大値問題が
苦手なままかも、、、
この書き方を身につければ
どんな二次関数の最大値、最小値の問題
が来ても怖いもの無しです!!!

この方法は
青チャートにも
記載されている方法です!!!
まずは
二次関数の問題ときたらこれ!!
基本形に直す!!

次に
二次関数の式が
下の凸か上に凸かを判断
最後に
図を書いて可視化して
場合分けをします!
範囲が動くパターンは
グラフが指定されています!!
なので先に式のグラフを書いてから
範囲を書くようにしましょう!!
そして
「ちょっと大袈裟だな!」
と思うぐらい描くと、特徴が分かります!!
下に凸の場合

上に凸の場合

たったこの3ステップを踏めば
誰でも書けるようになります!!
しっかりと図で
「可視化」することで
一目見ただけで理解できます!!
あとは、場合分けをして解答を作るだけ!!
例を見て見ましょう!
「aは定数とする。定義域0<=x<=aにおける関数
f(x)=x^2-4x+1 について最大値を求めよ。
①0<a<2 ②2<=a<4 ③a=4 ④4<a」
という問題です!
まず初めに
二次関数の問題!ときたら、、、
そう!!基本形に直します!

次に
下は凸か上に凸かの判断です!
今回は2乗の係数が「+」なので
下に凸のグラフですね!!
最後に
グラフを書いて場合分けをします!
今回の4つの場合は
この4つの図が書けますね!!

あとは
これを流れに沿って書くだけ!!
こんな感じになります!

この流れを覚えれば
誰でも回答を作れるようになります!!
これであなたも最大値最小値問題は
怖いもの無しです!!
今からでもできることとして!!
二次関数の問題を見つけたら
基本形に直しましょう!!!
その後この方法で
回答パターンを覚えば
最大値問題を
スラスラ解けるようになります!!